
This point is sometimes called half-stable because the force on one side points toward the fixed point.Ī practical application of the concept of stable equilibrium points is the force between two neutral atoms in a molecule. (b) A potential energy function with an unstable equilibrium point. (a) A potential energy function with a stable equilibrium point. The force at a position is equal to the negative of the slope of the graph at that position. The first is a stable equilibrium point (a), the second is an unstable equilibrium point (b), and the last is also an unstable equilibrium point (c), because the force on only one side points toward the equilibrium point.įigure 15.15 Two examples of a potential energy function. This point is an unstable equilibrium point.
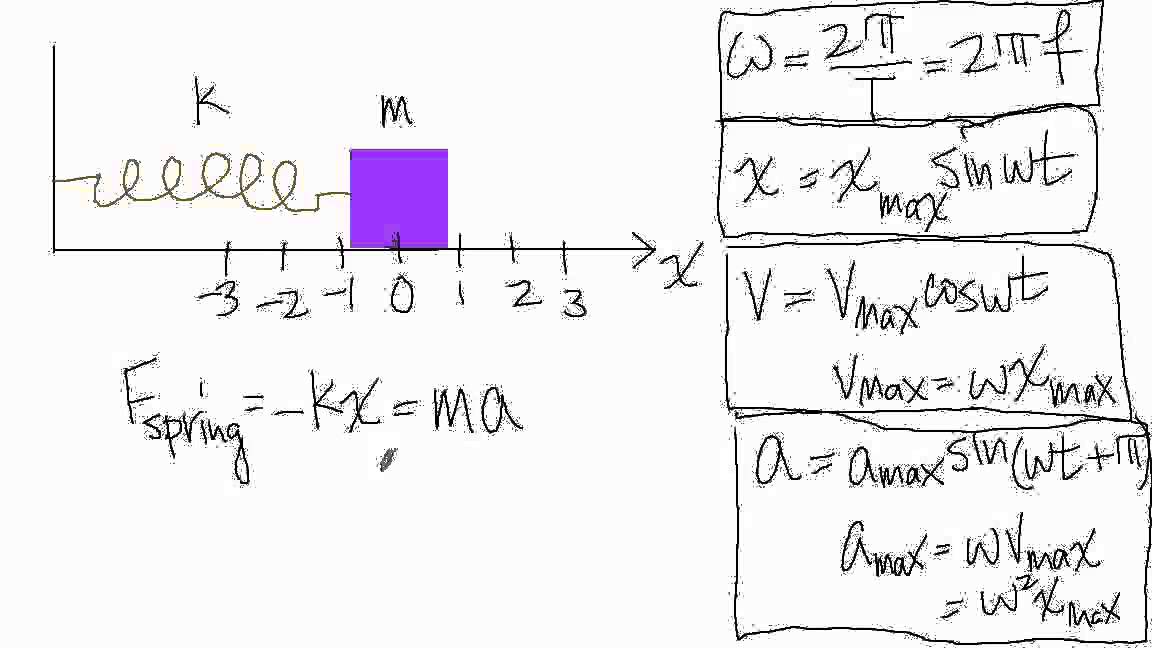
The reason is that the force on either side of the equilibrium point is directed away from that point. However, if the marble is disturbed slightly, it will not return to the equilibrium point, but will instead roll off the bowl. If the bowl is turned upside down, the marble can be balanced on the top, at the equilibrium point where the net force is zero. If the bowl is right-side up, the marble, if disturbed slightly, will oscillate around the stable equilibrium point. For an unstable equilibrium point, if the object is disturbed slightly, it does not return to the equilibrium point.Ĭonsider the marble in the bowl example. The stable equilibrium point occurs because the force on either side is directed toward it. If an equilibrium point is stable, a slight disturbance of an object that is initially at the stable equilibrium point will cause the object to oscillate around that point. (See Potential Energy and Conservation of Energy.) In a simple harmonic oscillator, the energy oscillates between kinetic energy of the mass K=\fracA are called the turning points. In this case, the block oscillates in one dimension with the force of the spring acting parallel to the motion:

This potential energy is the energy stored in the spring when the spring is extended or compressed. The force of the spring is a conservative force (which you studied in the chapter on potential energy and conservation of energy), and we can define a potential energy for it. If the only result is deformation, and no work goes into thermal, sound, or kinetic energy, then all the work is initially stored in the deformed object as some form of potential energy.Ĭonsider the example of a block attached to a spring on a frictionless table, oscillating in SHM. That is, whether you pluck a guitar string or compress a car’s shock absorber, a force must be exerted through a distance. To produce a deformation in an object, we must do work.

Hence, the motion of point P' is a simple harmonic motion. These characteristics are similar to the characteristics of a Simple Harmonic Motion. Therefore, \quad \text ) is acting in a direction opposite to the direction of displacement ( x ).

General conditions of simple harmonic motionĪ simple harmonic motion is an oscillatory motion. Restoring force must be acting in a direction opposite to the direction of displacement.Restoring force must be proportional to the displacement of particle from mean position.It should be a “to and fro” type of vibratory motion.Uniform Circular Motion is Simple Harmonic MotionĪ periodic oscillatory motion in which a particle moves to and fro about a mean position under the action of a restoring force which is directly proportional to its displacement from the mean position and is always directed towards the mean position, is called Simple Harmonic Motion.Ī simple harmonic motion possess following characteristics –.General conditions of simple harmonic motion.


 0 kommentar(er)
0 kommentar(er)
